© 2010
Автор – Олег Николаевич Розанов
«Вооруженные таким мощным орудием как законы Ньютона, вы можете вычислять не только такие простые явления, как качание груза, но и чрезвычайно сложные движения планет, причем с любой желаемой точностью. Нужна только машина знающая арифметику»
Р.Фейнман (42)стр.177.
В этой статье предлагаются очень простые арифметические расчёты с использованием классических законов И.Ньютона, которые очень убедительно помогут понять закономерность движения небесных тел по эллиптическим орбитам, без интерпретаций фантастического характера и сложных математических алгоритмов, а так же подчеркнуть универсальность классических законов в Микро, Макро и Мегамирах.
1. Закономерность изменения эллиптической орбиты в орбиту круговую, как следствие обратно пропорционального распределения центростремительной и центробежной силы, при движении к точкам афелия и перигелия.
Эта закономерность, движения небесных тел по эллиптическим орбитам, чётко просматривается при расчётах центробежной и центростремительной сил, любых планет или небесных тел в точкам перигелия и афелия. Для примера рассмотрим движение планеты Меркурий, с самой эллиптической орбитой, среди планет солнечной системы.
(Примечание) В этой статье под термином “большая полуось” подразумевается расстояние между центром тяжести (Солнца) и точкой афелия.
Исходные данные для расчётов по Меркурию:
Масса(меркурия) = 3,3022 × 1023(кг).
Масса(солнца) = 1,9891 × 1030(кг).
V(max) = 58 980(m/sec) – в точке перигелия.
V2(max)= 3478640400(m2/sec2) = 3,4786404 × 109(m2/sec2)
V(min)= 38 860(m/sec) – в точке афелия.
V2(min)= 1510099600(m2/sec2) = 1,5100996 × 109(m2/sec2)
R(малая полуось)= 46 001 210 000(м)= 4,6 001 210 000 × 1010(м).
R2(м.п.)= 2116111321464100000000(м2) = 21,16111321464100 × 1020(м2).
R(большая полуось) = 69 820 000 000(м) = 6,9 820 000 000 × 1010(м).
R2(б.п.)= 4874832400000000000000(м2) = 4,874832400000000 × 1021(м2).
G = 6,672 × 10 -11(Н × м2/ кг2).
Вычисление центробежной силы в точках перигелия и афелия.
В точке перигелия:
F (ц.б. меркурия) = M × V2/ R
3,3022 × 1023(кг) × 3,478640400 × 109(m2/sec2) / 46 001 210 000(м)
= 11,48716632888 × 1032/4,6 001 210 000 × 1010(м)
= 2,4971443857411576782436809814351 × 1022(н)
= 24,971443857411576782436809814351 × 1021(н).
В точке афелия:
F (ц.б. меркурия) = M × V2/ R
3,3022×1023(кг) × 1,510099600 × 109(m2/sec2)/ 69 820 000 000(м)
= 4,98665089912 × 1032/6,9 820 000 000 × 1010(м)
= 7,1421525338298481810369521627041 × 1021(н).
Вычисление центростремительной силы в точках перигелия и афелия.
В точке перигелия:
F (ц.c. меркурия) = M(меркурия) × M(солнца) × G / R2
3,3022 × 1023(кг) × 1,9891 × 1030(кг) × 6,672 × 10 -11/ 21,161 × 1020(м2)
= 6,56840602 × 1053(кг) × 6,672 × 10 -11/ 21,161 × 1020(м2)
= 43,82440496544 × 1042/ 21,161 × 1020(м2)
= 20,709876895851901230216580198078 × 1021(н).
В точке афелия:
F (ц.c. меркурия) = M(меркурия) × M(солнца) × G / R2
3,3022 × 1023(кг) × 1,9891 × 1030(кг) × 6,672 × 10 -11/4,8748324 × 1021(м2) =
43,82440496544 × 1042/4,8748324 × 1021(м2) =
8,9899306005761346790096824662116 × 1021(н).
Ц.б. сила в точке перигелия:
24,9714 × 1021(н) > Ц.с. сила 20,7098 × 1021(н),
Ц.б. сила. в точке афелия:
7,14215 × 1021(н) < Ц.с. сила 8,9899 × 1021(н).
Для большей уверенности вычислим эти силы, в двух точках, у планеты с меньшим эксцентриситетом – Венера.
В продолжение я не буду использовать понятие эксцентриситет, т.к. считаю, что намного проще применять отношение значений длин большой и малой полуосей т.к. это отношение так же указывает на эллиптичность любой орбиты и помогает очень просто определять максимальную и минимальную скорость движения планеты, которые в основном не указываются.
L(б.п.)/L(м.п.)= V(max)/V(min).
Данные взяты из Википедии:
Меркурий:
6,9820 × 1010(m) / 4,6001210 × 1010(m) ≈ 1,517
58 980(m/s) / 38 860(m/s) ≈ 1,51775
Земля:
1,52097701 × 1011(m) / 1,47098074 × 1011(m) ≈ 1,0339
30 270(m/s) / 29 270(m/s) ≈ 1,0341
Исходные данные для расчётов по Венере:
Как правило для планет указываются только среднюю линейную скорость движения.
V(средняя) = 35 020(m/sec)
L(б. полуось) / L(м. полуось) ≈
108 942 109 000(м) /107 476 259 000(м) ≈
1,01363882604064.
Следовательно:
V(max)/ V(min) ≈ 1,0136
V(max)+V(min)/2 = V(средняя) – т.е. 35 020(м/сек)
получаем следующие значения V(max) и V(min):
V(max) = 35257,198290858565202746561696644(м/сек),
V(min) = 34782,801709141434797253438303356(м/сек),
V2(max) = 1243070031,3209201312969962909159(м2/сек2),
V2(min) = 1209843294,7374523176962579284497(м2/сек2),
M(Венеры) = 4,8685 × 1024(кг),
R(малая полуось) = 107 476 259 000(м),
R(большая полуось) = 108 942 109 000 (м),
R2(м.п.) = 11 551 146 248 635 081 000 000(м2) = 1,1551146 × 1022(м2),
R2(б.п.) = 11 868 383 113 367 881 000 000(м2) = 1,1 868 38 × 1022(м2)
Вычисление центростремительной силы в точках перигелия и афелия.
В точке перигелия:
F (ц.c. Венеры) = M(Венеры) × M(солнца) × G / R2
4,8685 × 1024(кг) × 1,9891 × 1030(кг) × 6,672 × 10-11/1,1551146 × 1022(м2)
= 64,6112033112 × 1043/1,1551146 × 1022(м2)
= 5,5934884660329409891740584430746 × 1022(н).
в точке афелия:
F (ц.c. Венеры) = M(Венеры) × M(солнца) × G / R2
4,8685×1024(кг) × 1,9891 × 1030(кг) × 6,672 × 10-11/ 1,1 868 38 × 1022(м2)
= 64,6112033112 × 1043/1,1 868 38 × 1022(м2)
= 5,4439768832896508756473372150247 × 1022(н).
Вычисление центробежной силы в точках перигелия и афелия.
В точке перигелия:
F (ц.б. Венеры) = M × V2/ R
4,8685 × 1024 × 1243070031/ 107 476 259 000 =
= 605188644748,58996592194264423197 × 1022 / 107 476 259 000
= 5,63090537742470144892131614138 × 1022(н).
В точке афелия:
F (ц.б. Венеры) = M × V2/ R
4,8685×1024 × 1209843294 / 108 942 109 000
= 589012208042,9286608704231724654 ×1022 / 108 942 109 000
= 5,40665325326985051180185223388 ×1022(н).
Ц.б. сила в точке перигелия:
5,6309 × 1022(н) > Ц.с. сила 5,5934 × 1022(н).
Ц.б. сила в точке афелия:
5,4066 × 1022(н) < Ц.с. сила 5,4439 × 1022(н).
Очевидна закономерность обратно пропорционального распределение ц.б.с. и ц.с.с. и это даёт полное право утверждать, что происходит укорочение большой полуоси и отклонение точки перигелия от предыдущей, в противоположном направлении вращения планеты, эти изменения начинаются с точек равнодействия, при постоянной длине орбиты.
В продолжение рассуждений о «загадочной» теме смещения точек перигелия и афелия (орбиты Меркурия), основанной на не сложных арифметических расчётах , что в движении всех небесных тел, по эллиптическим орбитам, существует закономерность обратно пропорционального распределения центростремительной и центробежной силы, несложно догадаться, что на орбите имеются две точки местонахождения планеты, где эти силы уравниваются. Одна из точек находится после точки перигелия, а другая после точки афелия.
Для полной ясности и для редактирования графического изображения орбиты Меркурия, рассчитаю расстояние между центрами тяжести Меркурия и Солнца в двух точках равнодействия, где Сила центробежная и Сила центростремительная равны между собой.
Вычисление орбитальных точек равнодействия.
Дабы не утомлять дорогих читателей длинными рядами чисел, с расчётами для точек равнодействия, укажу только на конечные результаты, которые можно легко проверить подставляя их в формулы:
F = M(1) × V2/ R,
F = M(1) × M(2) × G / R2,
или с помощью объединенного д.у.:
Точка перигелия.
С этой точки начинается замедление движения планеты Меркурий, что удерживает планету на данной орбите, так как обратно пропорциональное распределение сил, после точки равнодействия, где центростремительная сила начинает превышать центробежную силу, возвращает движение планеты к Солнцу.
Точка равнодействия на отрезке движения планеты перигелий – афелий:
Ц.б. сила = Ц.с. сила = 11,51413803739118836 × 1021 (н).
в точке на расстоянии:
R = 61 693 910 372(м),
при скорости движения планеты:
V = 46 380(м/сек).
После точки афелия, происходит ускорение движения планеты Меркурий до точки перигелия, а с точки равнодействия – Ц.Б. сила начинает превышать Ц.С. силу, до точки равнодействия на промежутке движения планеты перигелий – афелий.
Точка равнодействия на отрезке движения планеты афелий – перигелий.
Ц.б. сила = Ц.с. сила = 14,95833675146708504 × 1021(н).
в точке на расстоянии:
R = 54 127 299 627(м),
при скорости движения планеты:
V = 49 516(м/сек).
Расчёты приблизительно указывают орбитальные точки равнодействия где Ц.б.с. и Ц.с.с. равны между собой, с которых начинается смещение траектории движения к новым точкам перигелия и афелия, как следствие обратно пропорционального распределения центробежной и центростремительной сил.
Стабилизированная орбита планеты Меркурий, если не произойдёт какого-либо столкновения с небесными объектами (астероид, комета), будет иметь следующие приблизительные параметры:
Окружность с радиусом:
R ≈ 57 910 604 999,5 (м),
и постоянной скоростью движения:
V ≈ 47 948 (м/сек),
где будет соблюдаться условие:
Ц.б.с. ≈ Ц.с.с. ≈ 13,2362373944291367 × 1021 (н).
Заключение.
- Изменение местоположения орбитальных точек перигелия и афелия, любой планеты, происходит из-за обратно пропорционального перераспределения центробежной и центростремительной силы, с момента прохождения точек равнодействия.
- Результаты данных вычислений объясняют устойчивое вращение небесных тел на своих орбитах, а так же опровергается утверждение И. Ньютона «что все планеты падают», но подтверждается универсальность его законов механики, которые применимы и в мегамире.
- Анализируя форму орбиты с помощью расположения точек равнодействия – даёт полное право утверждать, что смещение точек орбиты перигелия и афелия – направлено в противоположную сторону движения небесных тел.
Квазары – генераторы вещества галактик и антивещества антигалактик
Законы классической механики и о якобы невозможности их применения в расчетах небесной механики
- Уважаемые посетители, что-бы оставить свой комментарий — регистрация не предусматривается.
- Набор математических формул, в комментариях, редактируется в системе «LATEX». Формула открывается словом katex [в квадратных скобках] и закрывается /katex [в квадратных скобках].
- Если ваш комментарий имеет ссылку, он автоматом направляется в спам, для проверки. Без ссылок, все комментарии публикуются без задержек.
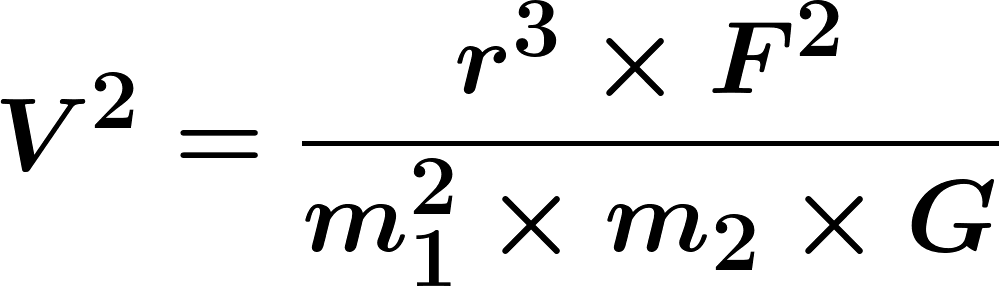
Только что это доказывает?
Почему в перигелии Меркурий не улетает на хрен из Солнечной системы? А в афелии не падает на Солнце? Что этому мешает?