© 2006
El Autor – Rozánov Nicolái Nicoláevich
Las traducciones de los títulos, de los artículos, de los libros, de las citaciones y declaraciones de los científicos – posiblemente no coinciden letra a letra con las traducciones oficiales, si tal existieran.
En el artículo de J. Brown y M. Row, “La estructura del nucleón”, publicado en la colección “Física en el extranjero”, ’84 “A” INVESTIGACIONES, Moscú “MIR” (pp. 31–59), en la sección: “¿Cuáles son las dimensiones del nucleón?”, basándose en la teoría cuark–gluón–mesón de los nucleones, se escribe lo siguiente:
“Se podría pensar que las dimensiones del nucleón se estiman mejor a partir de su factor de forma eléctrico, el cual caracteriza la distribución espacial de la carga en el nucleón y se determina en experimentos de dispersión elástica de electrones. Con este enfoque fueron determinadas con precisión las dimensiones de los átomos y de los núcleos. Pero, según uno de los modelos más recientes que vamos a considerar, en el nucleón existen dos regiones diferentes. En su región central, los cuarks casi sin masa se mueven prácticamente libres, interactuando débilmente entre sí; esto es la llamada libertad asintótica. En la región externa, de mayor tamaño, se encuentran los piones y otros mesones; a esta región la llamaremos nube mesónica. Diversos enfoques fundamentales, tales como las teorías de calibración en retículo, comienzan actualmente a esclarecer la cuestión de cómo y dónde los cuarks, gluones y otros constituyentes participan en la formación de la región de confinamiento de los cuarks, denominada “bolsa”. Sin embargo, por el momento estos cálculos no dicen con certeza de qué manera en el nucleón se produce la separación en dos regiones: el núcleo interno, compuesto por cuarks, y la nube mesónica externa».
De lo expuesto se deduce que la existencia de cuarks y gluones sería, supuestamente, un hecho experimental fundamental ((21) pp. 31–59). Sin embargo, para cualquier persona interesada en la teoría de partículas elementales, está absolutamente claro que esto no corresponde del todo a la realidad. Aunque en la sección “El modelo de bolsas del MIT” se afirma:
En el experimento que mostró de manera convincente que los nucleones están compuestos por cuarks, estos se comportaban como libres y sin masa. Se trató de un experimento de dispersión inelástica profunda de electrones a altas energías. Surge entonces la pregunta: ‘¿De dónde provienen las masas de los cuarks (m(q)) que mencionamos anteriormente?’ Por supuesto, solo considerábamos la región de bajas energías, y las constantes de acoplamiento dependen de los impulsos y se hacen mayores a bajos impulsos, de modo que es posible algún mecanismo mediante el cual los cuarks adquieran masa. En este sentido es interesante el modelo de bolsas del MIT (Instituto Tecnológico de Massachusetts), en el cual los cuarks u y d son casi sin masa (si se desprecia la pequeña masa de los cuarks u y d “de corriente”, igual a unos pocos megaelectronvoltios)…”.
“En el modelo de bolsas del MIT se postula que los cuarks no pueden salir de la bolsa, lo cual se expresa en la condición de frontera para la función de onda en el borde de la bolsa, correspondiente al radio (R) (MIT – Massachusetts Institute of Technology, 02139). De este modo, las partículas no pueden escapar de la bolsa. Con el tiempo, este confinamiento debería ser explicado por definición por alguna teoría adecuada, que todavía no existe. (!) Estableciendo la condición de frontera del modelo de bolsas del MIT se pueden buscar funciones de onda de los cuarks que, dentro de la bolsa, obedecerían la ecuación de Dirac para fermiones sin masa”.
El vacío físico es un enredo tremendamente complejo de espaguetis de colores –campos de calibración– con salsa de condensado cuark–antiquark. Para que los cuarks puedan existir localmente, debemos crear una burbuja, o bolsa, y para ello se necesita energía. Se asume que la energía es proporcional al volumen: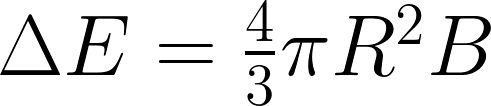
donde (B) es la “constante de la bolsa”.
Las energías de los quarks se pueden encontrar a partir de la condición de frontera del modelo de bolsas del MIT, con la cual se determinan los valores propios de energía. Para un quark en el estado fundamental con IS = ½, tenemos:
E(Q) = 2,04\ \hbar\ \frac{C}{R}.
Por consiguiente, la energía de la bolsa con tres quarks es igual a:
E = \frac{4}{3}πR3 B + (3 × 2,04\ \hbar\ \frac{C}{R}).
Aquí se añaden además diversos términos adicionales, pero esta fórmula expresa la esencia del modelo. El parámetro (B) se elige de modo que, en el mínimo respecto a (R), la energía de la bolsa sea igual al valor experimental de la masa del nucleón:
m_{\left(n\right)}{\times}C^2.
Como no es difícil darse cuenta, el término con (R³) impide que la bolsa se expanda demasiado, mientras que el término con (1/R) es, en esencia, la energía cinética que no deja que la bolsa colapse. (En el fondo, fuerzas centrípetas y centrífugas (aut.)…).
«Dado que el parámetro (B) se utiliza para que el mínimo de la energía se encuentre en el valor adecuado, el parámetro natural con dimensión de energía resulta ser la magnitud:
\ \hbar\ \frac{C}{R} – de bolsa»
((21) p.49).
Pero:
\ \hbar\ \frac{C}{R} – de bolsa»
esto es la relación de indeterminación de Heisenberg:
((20) p. 465).
De donde:
– esta relación es la que el autor del presente trabajo considera fundamental para el cálculo de los factores de forma de las partículas de materia y antimateria, es decir, protones, electrones y sus antipartículas. (Véase Apéndice-1).
Partiendo de los postulados de la teoría especial de la relatividad extendida de Recami ((5) pp.53–123), así como de los trabajos citados en las fuentes 3, 4, 8, 9, 10, 7, 13, se debe reconocer que la sustancia y la antisustancia en el Universo están constituidas por partículas estables (t = ∞), que poseen masa en reposo (en su propio sistema de referencia) ((20) p.72) y un incremento relativista de masa – Δm, además de una carga eléctrica elemental unitaria – \left (\overset{\pm}{e}\right) (aut.).
En el Universo solo existen cuatro de tales partículas:
-
protón – \left ( \overset{+}{p} \right ), positrón – \left ( \overset{+}{e} \right ) – bradiones (B),
con carga elemental (+1), -
antiprotón – \left ( \overset{-}{p} \right ), electrón – \left ( \overset{-}{e} \right ) – taquiones (T),
con carga elemental (–1).
El neutrón y el antineutrón son partículas compuestas.
El neutrón consiste en:
\left ( \overset{+}{p} \right ) – un bradión y \left ( \overset{-}{e} \right ) – reinterpretado en la región tipo-tiempo del cono de luz del taquión,
mientras que el antineutrón consiste en:
\left ( \overset{-}{p} \right ) – un taquión y \left ( \overset{+}{e} \right ) – reinterpretado en la región tipo-espacio del cono de luz del bradión (3,4,5,13).
Los bradiones entre sí y los taquiones entre sí se repelen, mientras que los bradiones con los taquiones se atraen mediante la fuerza de Coulomb.
Todos los núclidos están constituidos por diadas:
\left(\overset{\pm}{p}\right ) + \left(\overset{\mp}{e}\right )
(38,32,29),
en las cuales la cantidad de nucleones – \left(\overset{\pm}{p}\right ) y leptones – \left(\overset{\mp}{e}\right )
es exactamente igual. Al mismo tiempo, la diada puede estar formada por un electrón (o positrón) en la corteza atómica y un protón (o antiprotón) en el núcleo, o bien por neutrones (o antineutrones) en el núcleo, que también son diadas
\left(\overset{\pm}{p}\right ) + \left(\overset{\mp}{e}\right ) ,
pero más estrechamente ligados entre sí. Precisamente el campo de las diadas constituye el campo gravitacional. (Véanse Apéndices-2,3,4,5,6,7 y Ejemplos-1,2,3,4,5,6,7,8).
- Dejar el comentario – no hace falta registro.
- Para insertar la ecuación en los comentarios– utilizar el sistema «LATEX«. La fórmula se abre con la palabra – katex [entre] y se cierra – katex [/entre].
- Comentarios con enlaces – entraran en el correo no deseado, para verificar el contenido.