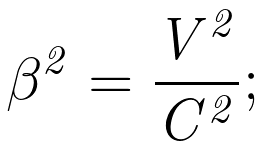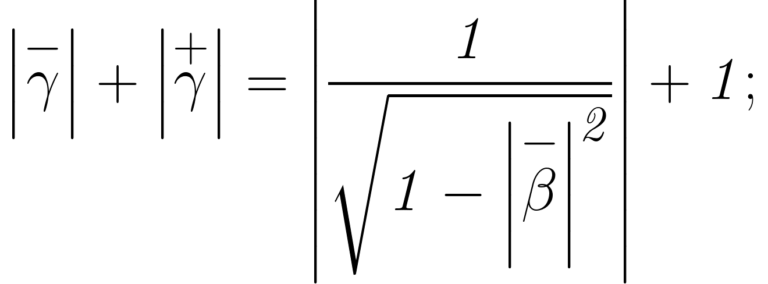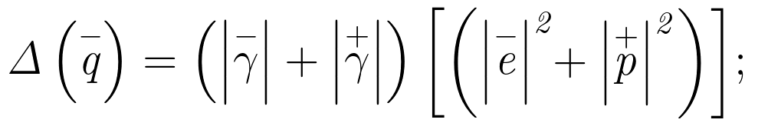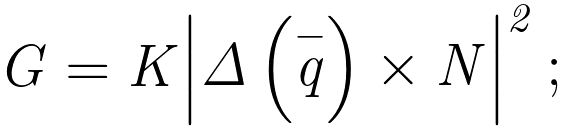![]()
© 2006
Los Autores – N.N.Rozánov, O.N.Rozánov
Las traducciones de los títulos, de los artículos, de los libros, de las citaciones y declaraciones de los científicos – posiblemente no coinciden letra a letra con las traducciones oficiales, si tal existieran.
«Ya en 1920, Rutherford planteó la hipótesis de la posible existencia de una partícula sin carga, compuesta por un protón y un electrón estrechamente unidos, formando una diada neutra» ((27)pág.6).
«Aplicando las leyes de conservación de la energía y el momento, Chadwick demostró que la radiación primaria tiene una masa cercana a la del átomo de hidrógeno (con un error de aproximadamente el 10%) y carece de carga»… «Chadwick envió su artículo «Posible existencia del neutrón» a imprenta el 17 de febrero de 1932. Este día es considerado, con razón, el día del descubrimiento del neutrón». ((27)pág.6). Chadwick también supuso que el neutrón era una partícula compuesta (27).
«Sin embargo, la convicción de que el neutrón era, en efecto, una «partícula elemental» se formó ya en 1932, tras la aparición del modelo de núcleo protón-neutrón de Ivanenko y Heisenberg»… «Heisenberg afirmó de forma más contundente que el neutrón no solo era una «partícula elemental», sino que el protón y el neutrón eran dos estados (cuánticos) de una misma partícula». Esta afirmación es, en la práctica, generalmente aceptada incluso hoy en día ((27)pág.8).
Estimados lectores, desde 2006 hasta 2020, en esta página se publicó un trabajo con cálculos de los parámetros del neutrón basados en la «distribución de cargas en el neutrón», cuya representación gráfica se encuentra en la página Anexo-1. En estos cálculos existen resultados muy contradictorios, con los que no estoy de acuerdo y, para los interesados, publicaré el archivo PDF. La versión que se expone a continuación es más simplificada, donde los cálculos se basan en el Δm del neutrón (n).
Así pues, el incremento de masa generalmente aceptado es:
Δm = 0,0013946596935 × 10-27(kg) = 13,946596935 × 10-31(kg).
Este incremento de masa se distribuye entre el protón y el electrón, y para ello hay que tener en cuenta la proporcionalidad de la energía y la masa de estas partículas, es decir, en el protón estos valores de propiedades superan en ~1836 veces los valores de estas propiedades en el electrón, y también hay que considerar que la velocidad lineal de movimiento de estas partículas no puede exceder la velocidad de la luz (en el par \left(\overset{\mp}{p}\right)+\left(\overset{\pm}{e}\right) del neutrón o antineutrón, la velocidad lineal de movimiento de los leptones es máxima).
Considerando la relación de masas y energías del electrón y el protón (\left(\overset{\mp}{p}\right) > \left(\overset{\pm}{e}\right) en ~1836 veces), determinamos el incremento de masa para el protón y el electrón en la diada neutrónica.
Para el electrón:
13,946596935 × 10-31(kg) / 1836 = 0,00759618569444444444444444 × 10-31(kg).
Para el protón:
13,946596935 × 10-31(kg) – 0,0075961856944444 × 10-31(kg)
= 13,939000749305555555555555555556 × 10-31(kg)
= 0,0013939000749305555555555555556×10–27(kg).
Con la ayuda de la regularidad:
T = Δm × c2
determinamos los valores de las energías cinéticas poseídas por \left(\overset{\mp}{p}\right) y \left(\overset{\pm}{e}\right) en la diada neutrónica o antineutrónica:
\left(\overset{\pm}{e}\right) –
T_{\left(\overset{\pm}{e}\right)} = 0,007596185694 × 10-31(kg) × 8,98755182 × 1016(m²/s²) = 6,827111393047555555555×10-17(J).
\left(\overset{\mp}{p}\right) –
T_{\left(\overset{\mp}{p}\right)} = 13,939000749306 × 10-31(kg) × 8,98755182 × 1016(m²/s²) = 1,25277494062422644 × 10-13(J).
Habiendo determinado los valores de las energías cinéticas, \left(\overset{\mp}{p}\right) y \left(\overset{\pm}{e}\right), determinemos el cuadrado de la velocidad lineal de las partículas en la diada utilizando la ecuación:
T = m‘ × V2 / 2
de donde:
V2 = 2T / m‘.
Pero para empezar, precisemos la masa de las partículas elementales con incremento relativista en la diada (n) – \left(\overset{\mp}{p}\right) y \left(\overset{\pm}{e}\right), y comencemos con \left(\overset{\pm}{e}\right):
m‘ = Δm + m(0)
0,007596185694444 × 10-31(kg) + 9,10938356 × 10-31(kg) = 9,1169797456944444444444444444444 × 10-31(kg).
V² = 2 × 6,8271113930476 × 10-17(J) / 9,1169797456944 × 10-31(kg)
= 1,497669531682727548411287709872 × 1014(m²/s²).
V = 1,2237930918593745471115603387766 × 107(m/s).
Determinamos los mismos parámetros para \left(\overset{\mp}{p}\right):
Δm = 0,0013939000749305555555555555556 × 10-27(kg),
m(0) = 1,6726219 × 10-27(kg),
m‘ = Δm + m(0)
0,00139390007493 × 10-27 + 1,67262191 × 10-27
= 1,6740158000749305555555555555556 × 10-27(kg).
Ahora determinemos la velocidad lineal de \left(\overset{\mp}{p}\right) utilizando la ecuación:
V\left(\overset{\mp}{p}\right) = V\left(\overset{\pm}{e}\right) × (m’\left(\overset{\pm}{e}\right)/ m’\left(\overset{\mp}{p}\right))
1,2237930918 × 107(m/s) × ( 9,11697974569 × 10-31(kg) / 1,67401580007 × 10-27(kg))
= 1,2237930918 × 107(m/s) × 5,4461730560048 × 10-4
= 6,6649889630093617529810283725466 × 103(m/s)
= 0,0006664988963009361752981028372 × 107(m/s).
Restemos la velocidad lineal del protón de la velocidad de movimiento del electrón y obtendremos el valor de la velocidad que excita \Delta\left(\overset{-}{q}\right) en la diada, y al mismo tiempo igualaremos el valor \overset{+}{\gamma} a 1:
1,223793091859 × 107(m/s) – 0,000666498896 × 107(m/s)
= 1,2231265929630736109362622359394 ×107(m/s)
V² = 1,4960386624134563521067194958075 × 1014(m²/s²).
A continuación, determinaremos el valor de \left(\overset{-}{\beta}\right)^2 para el electrón:
1,4960386624 × 1014(м 2/с 2) / 8,98755182 × 1016(м 2/с 2)
= 0,16645674955490341218491238649765 × 10-2
= 0,0016645674955490341218491238649765.
Ahora determinaremos el valor de \overset{-}{\gamma}, y dado que \overset{+}{\gamma} = 1:
\overset{-}{\gamma} = (1 /(1 – 0,0016645674955490341218491238649)½)
=(1 /(0,9983354325044509658781508761351)½)
=(1 / 0,99916736961554692570192054500231)
=1,0008333242355316791042893102984;
entonces:
\left|\overset{-}{\gamma} \right|+\left| \overset{+}{\gamma}\right|
1,000833324235531 +1 = 2,000833324235531.
Por consiguiente, \Delta\left(\overset{-}{q}\right):
\Delta\left(\overset{-}{q}\right) = 2,000833324235531 × ((1,6021892×10-19)2 + (1,6021892×10-19)2) =
= 2,000833324235531 × 5,13402046519328×10-38(cl)
= – 10,27231923406591769905015843168 ×10-38 (cl)
= – 1,027231923406591769905015843168×10-37(cl).
Este valor será necesario para calcular \Delta\left(\overset{-}{q}\right) de otros isótopos.
El siguiente paso es el cálculo del número de neutrones en un kilogramo de masa inercial de «neutronio».
m(n) = 1,00866522(uma)
((38)pág.62).
En kilogramos (SI):
m(n) = 1,00866522(uma) × 1,6605655 × 10-27(kg)
= 1,67495466538191×10-27(kg),
N(n/kg) = 1(кg) / 1,67495466538191×10-27(kg)
= 5,97031084284294 × 1026.
A continuación:
K – es el coeficiente eléctrico en el sistema SI – 8,9875517873 × 109(N×m²/C²).
N – es el número de neutrones en 1(kg) de masa inerte de neutronio.
8,9875517873 × 109|- 1,027231×10-37(c) × 5,97031084284294 × 1026|2=
8,9875517873 × 109|- 6,1328938904287832956 × 10-11|2=
8,9875517873 × 109 (37,612387471258697 × 10-22) =
338,04328024193122967684414145732 × 10-13(N × m2/ kg2),
G(n) = 3,380432802419312 ×10-11(N × m2/ kg2).
- Estimados visitantes, para dejar su comentario, no se requiere registro.
- La edición de fórmulas matemáticas en los comentarios se realiza en el sistema «LaTeX». Una fórmula se abre con la palabra
katex[entre corchetes] y se cierra con/katex[entre corchetes]. - Si su comentario contiene un enlace, se enviará automáticamente a la carpeta de spam para su revisión. Sin enlaces, todos los comentarios se publican sin demora.