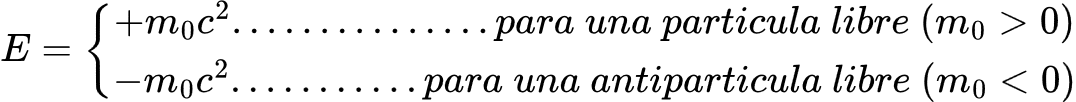![]()
© 2006
El Autor – Rozánov Nicolái Nicoláevich
Las traducciones de los títulos, de los artículos, de los libros, de las citaciones y declaraciones de los científicos – posiblemente no coinciden letra a letra con las traducciones oficiales, si tal existieran.
«El vacío físico constituye un medio polarizado, heterogéneo y omnipresente, compuesto por el vacío físico homogéneo-absoluto y dos vacíos físicos modificados de la sustancia y de la antisustancia. Las formaciones locales de uno u otro vacío modificado (denominadas por el autor «dominios de vacío») flotan en el medio ilimitado del vacío físico absoluto.» (V. L. Dyatlov (4) – de la anotación).
En el artículo — «La teoría de la relatividad y sus generalizaciones» de E. Recami ((5) págs. 53-128), se afirma:
«De la exigencia de que los sistemas de referencia superlumínicos tengan sentido, se sigue que deben existir objetos y taquiones que se encuentren en reposo con respecto a — S y con respecto a — s respectivamente. Del hecho de que los luxones L poseen la misma velocidad para cualquier observador — s o S, se puede concluir que un bradión B(S) , con respecto a — S, representará un taquión T(s) con respecto a cualquiera de los sistemas — s, y viceversa:
B(S) = T(s) , T(S) = B(s) , L(S) = L(s).
Esto concuerda con el principio de dualidad, que ahora complementamos con la afirmación: «se supone que en los sistemas de referencia — S existen exactamente los mismos objetos físicos que en los sistemas — s, y viceversa».
Para concluir, señalemos que, cuando en los sistemas — s y S se observa el mismo acontecimiento, los vectores de tipo tiempo se transforman en vectores de tipo espacio y viceversa, al pasar de — s a S y de S a s. Por otro lado, es bien sabido que las transformaciones de Lorentz ordinarias de s1 a s2 o de S1 a S2 conservan el tipo del 4-vector.
Por lo tanto, se puede decir que las transformaciones de Lorentz sublumínicas deben ser tales que:
β ≡ u / с ,
c2t‘2+ (ix’)2 = + [c2t2+(ix)2], β2 < 1, (16 a),
mientras que las transformaciones de Lorentz superlumínicas (SLT), de — s a S o de S a s, deben ser tales que:
c2t‘2+(ix’)2 = – [c2t2+(ix)2], β2 > 1, (16 б)».
β ≡ u / с, β2 < 1,
preservan la forma cuadrática de Minkowski:
ημν x′μ x′ν = ημν xμ xν, (16a)
donde la métrica es:
ημν = diag(−1,+1,+1,+1).
En cambio, las transformaciones de Lorentz superlumínicas (SLT), de — s a S o de S a s, deben satisfacer:
ημν x′μ x′ν = – ημν xμ xν, β2 > 1 (16b)
Aquí el signo negativo indica que un intervalo de tipo tiempo se transforma en uno de tipo espacio y, recíprocamente, un intervalo de tipo espacio se transforma en uno de tipo tiempo bajo una SLT.
Por supuesto, los taquiones también poseerán masas en reposo reales, ya que constituyen partículas ordinarias con respecto a sus propios sistemas de reposo – f, donde f – son sistemas de referencia supralumínicos.
A partir de la ecuación (16 b), aplicada al vector de los cuatro impulsos de los taquiones, se puede obtener de inmediato la relación:
E2 – P2 = -m_{0}^{2} < 0
((m0)- sustancial).
Por eso tenemos:
Recordemos que cualquier transformación de Lorentz supralumínica proyecta la región interior del cono de luz (P2 = 0) sobre su región exterior, y viceversa.
Cabe señalar:
a) La velocidad de la luz conserva, por supuesto, su carácter de parámetro cinemático límite de nuestro cosmos tetradimensional (aun cuando se sepa que dicho límite posee dos «lados»), así como su función en la comparación de las unidades de longitud y de tiempo entre distintos observadores.
b) Los taquiones se desaceleran al aumentar su energía y se aceleran al disminuirla.
En particular, para reducir la velocidad de los taquiones hasta el límite inferior С, es necesaria una energía infinita. Por otro lado, cuando la celeridad de un taquión tiende al infinito, su energía tiende a cero. Esto impide la violación del postulado general según el cual «la energía solo puede transmitirse a una velocidad finita», puesto que el taquión posee energía nula precisamente para aquellos observadores ante los cuales aparece con celeridad infinita.
Obsérvese que un bradión puede presentar un momento lineal nulo y una energía mínima:
m0 × C2,
mientras que un taquión puede presentar energía nula y un momento lineal mínimo:
P0 × C,
Sin embargo, los bradiones (B) no pueden existir con energía nula, del mismo modo que los taquiones (T) no pueden existir con momento lineal nulo respecto a los observadores para quienes se manifiestan como taquiones. De ello se deduce que la celeridad infinita solo puede atribuirse a los taquiones que corresponden a la intersección del hiperboloide con el plano (E = 0) ((5), p. 72…).
Consideremos un taquión que posee una masa en reposo (m0) en su propio sistema de referencia y que se desplaza con respecto a nosotros con velocidad − u. En tal caso, observaremos la masa:
( β2 > 1 ), m0 – sustancial.
Es evidente que a los taquiones se les deben atribuir masas en reposo reales, y no puramente imaginarias, siempre que se tengan en cuenta las correspondientes transformaciones de Lorentz supralumínicas ((5), p. 74).
«Por supuesto, las leyes físicas en la teoría especial de la relatividad pueden escribirse en una forma universal, válida tanto para bradiones como para taquiones, es decir, en una formulación que coincide necesariamente con la forma habitual en el caso de los bradiones. Por ejemplo, la ecuación (24), presentada en forma G –covariante:
\left (\beta^2\ {_{<}^{>}}\ 1\right ), m0 – sustancial».
En la sección 5.1. Antisustancia, ((5) pág. 78), E. Recami escribe:
«Arriba se mostró que el principio de reinterpretación (RJP) excluye cualquier transmisión de información al pasado, incluso con la ayuda de taquiones, y al mismo tiempo permite predecir —simplemente por consideraciones de relatividad— la existencia de la antisustancia» ((5) pág. 87…).
«El principio de reinterpretación (RJP)» debe denominarse a la propiedad de las partículas (elementales) de la materia, consistente en que «no existen objetos con velocidad negativa que se muevan hacia adelante en el tiempo. Cualquier objeto (P) con energía negativa, que se mueva hacia atrás en el tiempo, puede y debe ser reinterpretado como su antiobjeto (P–), moviéndose en la dirección opuesta en el espacio, pero dotado de energía positiva y avanzando hacia adelante en el tiempo. Observemos que de nuestros tres postulados se sigue:
-
No existen objetos con energía positiva que se muevan hacia atrás en el tiempo.
-
No sólo podemos, sino que debemos aplicar el principio de reinterpretación. En efecto, puesto que pertenecemos al mundo macrofísico y, por lo tanto, debemos “explorar” el espacio-tiempo en la dirección positiva de t, no podemos ni siquiera “ver” una partícula que se mueve hacia atrás en el tiempo: siempre la veremos como su antipartícula “reinterpretada”, moviéndose hacia adelante en el tiempo.
-
Como ya se mencionó, el tercer postulado exige que las señales físicas sean transportadas únicamente por objetos que se muevan hacia adelante en el tiempo o, lo que es equivalente, sólo por objetos con energía positiva. Ahora está claro que nuestro principio de reinterpretación garantiza, al excluir la transmisión de información hacia el pasado, la validez de la ley de causalidad retardada (las causas preceden a sus efectos)» ((5) pág. 60).
Si recordamos de qué manera las antipartículas se obtienen a partir de sus correspondientes partículas, se puede concluir que a las antipartículas debe atribuirse formalmente masas en reposo negativas (pero, naturalmente, masas y energías relativistas totales positivas). Recordemos para mayor claridad que, en forma covariante, para cualquier partícula libre:
E = P0 = m0 u0 c2 ,
donde u0 — es la componente temporal de la 4-velocidad. La transformación de Lorentz no ortócrona — L, que realiza únicamente el cambio de signo de todas las componentes temporales:
E’ = – E’ = m0 (-u0 )c2 = – m0 u0 c2.
Como resultado, aplicando el principio de reinterpretación de manera que se obtenga la antipartícula correspondiente, finalmente tenemos, para la antipartícula:
E’ = – E’ = (-m0 )(-u0 )c2,
lo que implica que la antipartícula permanece con masa en reposo negativa. Por consiguiente, se puede escribir:
Así que siempre:
E = + |m0| c2
y si se asignan correctamente energías positivas, tanto a los electrones \left ( \overset{-}{e}\right ) como a los positrones \left (\overset{+}{e} \right ), entonces la ecuación libre de Dirac conduce a oposiciones para:
\left ( \overset{-}{e}\right ) и \left (\overset{+}{e} \right ),
como corresponde, sólo con la condición:
m0 (fermión) = -m0 (antifermión) ((5) página 62).
De las citas anteriores, tomadas del artículo de E. Recami, se debe reconocer:
a) Las partículas “positivas” (protón y positrón) — bradiones,
b) Las partículas “negativas” (antiprotón y electrón) — taquiones.
De acuerdo con la teoría de Dyátlov (4),
los dominios de sustancia y antisustancia son completamente equivalentes y «flotan libremente» en todo el espacio del universo (Vacío astrofísico), estando separados entre sí por el cono de luz (fig. 1), es decir, en un estado de superposición.
Los bradiones, en su propio sistema de referencia y en ausencia de fuerzas externas, poseen energía de reposo:
E(B) = m0 × C2, V(B) = 0,
mientras que los taquiones, en su propio sistema de referencia, poseen impulso:
P(T) = – m0 × C
y una velocidad:
V0(T) = 0,
![]()
ya que, en este caso, el módulo del momento resulta ser:
|P(T)| = m0 × C ((5) pag.65).
- Dejar el comentario – no hace falta registro.
- Para insertar la ecuación en los comentarios– utilizar el sistema «LATEX«. La fórmula se abre con la palabra – katex [entre] y se cierra – katex [/entre].
- Comentarios con enlaces – entraran en el correo no deseado, para verificar el contenido.