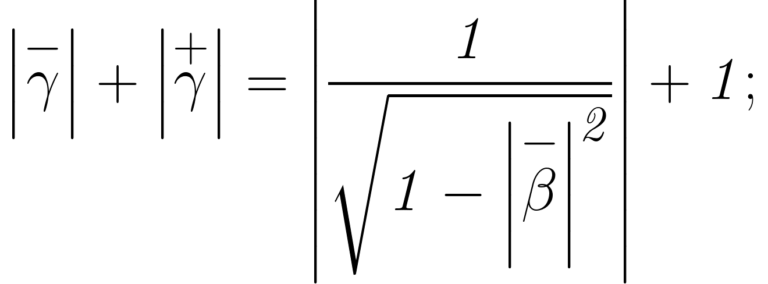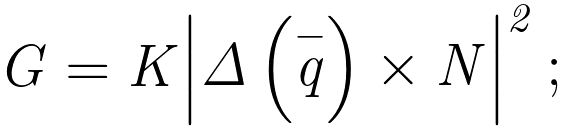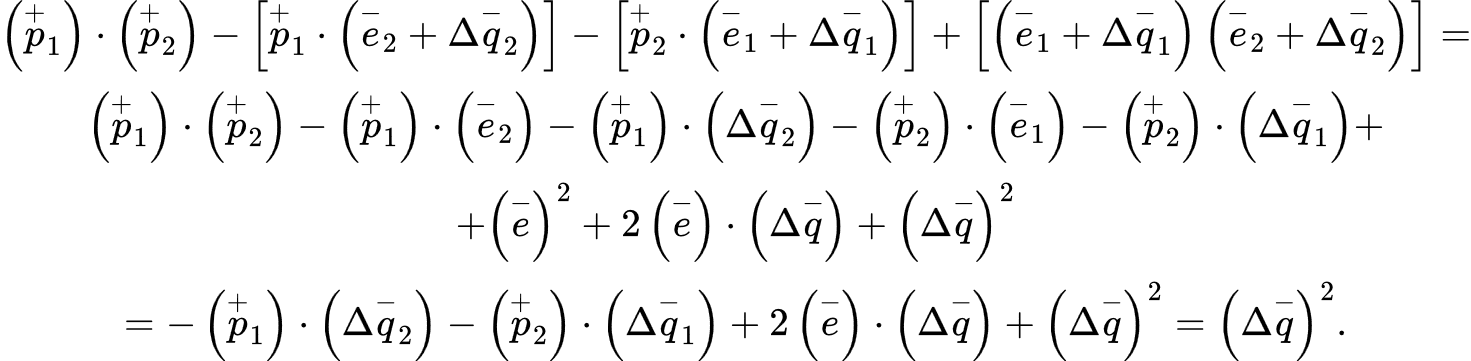© 2006
Los Autores – N.N.Rozánov, O.N.Rozánov
Las traducciones de los títulos, de los artículos, de los libros, de las citaciones y declaraciones de los científicos – posiblemente no coinciden letra a letra con las traducciones oficiales, si tal existieran.
Estimados lectores, esta es la versión actualizada del cálculo del valor de la carga electrodinámica negativa adicional (coeficiente gravitacional (- Δq)) para el átomo de protio, cuyo algoritmo ha sido simplificado. La versión de 2006, para los interesados, estará disponible en formato PDF.
Como base para el cálculo se utiliza el valor de la energía de enlace del átomo y, dado que:
1(eV) = 1,6021892 × 10-19(j)
respectivamente, la energía de enlace del par protón-electrón (antiprotón-positrón) en julios es:
E(¦H) = 13,62323824 (eV) = 2,182700518 × 10-18(J).
Considerando la relación de masas y energías del electrón y el protón (\left(\overset{\mp}{p}\right) > \left(\overset{\pm}{e}\right) en ~1836 veces), calculamos la distribución de las energías cinéticas en el par para el electrón:
2,182700518 × 10-18(J) / 1836 = 0,001188835 × 10-18(J)
1,18883470479302832244008714597 × 10-21(J)
y para el protón:
2,182700518 × 10-18(J) – 0,001188835 × 10-18(J) = 2,181511683 × 10-18(J).
A continuación, estableceremos el cuadrado de la velocidad lineal, para el electrón y el protón, utilizando la ecuación:
T = m‘ × V2 / 2
de donde:
V2 = 2T / m‘,
donde la masa relativista es igual a:
m‘ = m(0) + (T/C2)
ya que:
Δm = T / C2.
1 (uma) = 1,660 539 066 605 × 10-27(kg) – Wikipedia, valor recomendado desde 2018.
\left ( \overset{\pm}{e} \right ) = 5,4857990906516 × 10-4 (uma).
m(0) = 1,6605390666 ×10−27(кg) × 5,4857990906 ×10-4(uma)
= 9,109383701573165645249818 × 10− 31(кg).
Δm = T/C2 = 1,1888347048×10-21(J) / 8,98755182 × 1016(м 2/seg 2)
= 0,13227569961238101906600046128802 × 10-37(кg)
Δm = 0,000000132275699612381019 × 10-31(кg).
m‘ = 9,1093837015 × 10−31(кg) + 0,0000001323 × 10-31(кg) =
= 9,109383833848865257630837 × 10-31(кg).
= 0,0009109383833848865257630837 × 10-27(кg)
V2 = 2T / m‘ = 2 × 1,1888347047 × 10–21(J) / 9,1093838338 × 10-31(кg)
= 0,26101319836266598658835996234983 × 1010 (m2/seg2)
= 26,101319836266598658835996234983 × 108(m2/seg2).
V = 5,1089450805686489253191027290037×104(m/seg).
\left ( \overset{\mp}{p} \right ) = 1,007 276 466 621(53) (uma).
m(0) = 1,660 539 066 6 × 10−27(кg) × 1,007 276 466 6(uma)
= 1,67262192369689786399700565 × 10−27(кg).
Δm = 2,182700518 × 10-18(J) / 8,987552 × 1016(m2/seg2)
= 0,242858179624440559565052 × 10-34(кg)
= 0,0000000242858179624440559565052 × 10-27(кg).
m‘ = 1,67262192369 × 10-27(кг) + 0,000000024285817 × 10-27(кg)
= 1,6726219479827158264410616065052 × 10-27(кg).
La velocidad lineal del protón se calcula utilizando la ecuación:
V\left(\overset{\mp}{p}\right) = V\left(\overset{\pm}{e}\right) × (m‘\left(\overset{\pm}{e}\right) / m‘\left(\overset{\mp}{p}\right))
9,1093838338 × 10-31(кg) / 1,6726219479 × 10-27(кg) × 5,1089450805 × 104(m/seg)
= 5,4461702148 × 10-4(кг)× 5,1089450805 × 104(m/seg)
= 27,824184527222679361551577751067(m/seg).
= 0,0027824184527222679361551577751 × 104(m/seg).
Restamos la velocidad lineal del protón de la velocidad de movimiento del electrón y obtenemos el valor de la diferencia de velocidad que corresponde a la excitación \Delta\left(\overset{-}{q}\right) en la diada, y al mismo tiempo igualamos el valor \overset{+}{\gamma} a 1:
5,108945080 × 104(m/s) – 0,002782418452 × 104(m/s)
= 5,1061626621159266573829475712286 × 104(m/s)
o bien:
V² = 26,072897131986806982931986037314 × 108(m²/s²).
Cálculo del valor de \left(\overset{-}{\beta}\right)^2 para el electrón:
β2 = V2 / C2
26,072897131 × 108(m2/s2)/ 8,98755182 × 1016(m2/s2)
= 2,9010010350056381630889985830773 × 10-8
= 0,00000002901001035005638163089.
Pasemos a los cálculos:
((28) pag.180. (40) pag.209).
\overset{-}{\gamma} = 1 /(1 – 0,00000002901001035005638163089)½)
= 1 /(0,99999997098998964994361836911)½
= 1 /0,999999985494994719774220094866
= 1,000000014505005490620961136295.
\left|\overset{-}{\gamma} \right|+\left| \overset{+}{\gamma}\right|
1,000000014505 +1 = 2,000000014505005490620961136295.
A continuación:
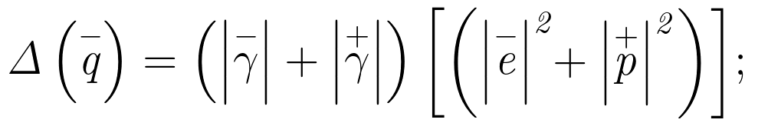\Delta\left(\overset{-}{q}\right) = 2,00000001450500549 × ((1,6021892 × 10-19)2 + (1,6021892×10-19)2)
= 2,00000001450500549 × 5,13402046519328 × 10-38(c)
= 10,268041004855555036588907492935 × 10-38 (c)
= – 1,0268041004855555036588907492935 × 10-37(c).
Número de átomos en un kilogramo de H₂:
0,000910938383 × 10-27(кg) + 1,6726219479827 × 10-27(кg)
= 1,6735328863661007129668246902052 × 10-27(кg).
N(at/kg)= 1 / 1,6735328863661007129668246902052 × 10-27(кg)
= 0,5975383024419639647589278802372 × 1027(at/kg)
= 5,9753830244196396475892788 × 1026(at/kg).
Por lo tanto, el coeficiente G para el hidrógeno es:
donde
K – coeficiente eléctrico en el sistema SI – 8,9875517873 × 109 (N×m²/c²)
N – número de átomos ¦H en 1(kg) de masa inerte de H₂:
8,9875517873 × 109|- 1,0268041 × 10-37(c) × 5,9753830244196 × 1026|2
= 8,9875517873 × 109|- 6,13554779144586622464409 × 10-11|2
= 8,9875517873 × 109 |37,644946701116246740591916353762 × 10-22 |
338,33590800643056229847467728519 × 10-13(N×m2/kg2);
G(¦H) = 3,3833590800643056229847467728519 × 10-11(N×m2/kg2).
Por consiguiente, la masa inercial del protio en el Universo es aproximadamente dos veces mayor, al comparar el resultado obtenido con las mediciones más precisas de la “constante gravitacional” (publicadas en Phys. Rev. Lett. 2003. 91. Nº20) para el cobre y el acero aleado.
Dado que todos los objetos sustanciales del Universo están formados por dos partículas —el protón y el electrón—, y los objetos de antisustancia por antipartículas —el antiprotón y el positrón— ((5) pág. 42–128,13), las leyes del megamundo son las mismas que las del micromundo: el principio de incertidumbre de Heisenberg, la ley del cuadrado inverso de la distancia y el teorema del virial (de Clausius).
«…El resultado del cálculo de la constante gravitacional del protio y del antiprotio, constituyentes de la sustancia y la antisustancia del Universo, resuelve el problema de la masa “oculta”, o “oscura”, o más precisamente, la masa “virial”:
m(r) = rv² / G,
donde:
m(r) — masa dentro de un volumen esférico de radio (r).
V(r) — velocidad de rotación a una distancia (r) del centro (de gravedad).
G — constante de gravitación».
«…Si la masa principal está concentrada en un volumen de radio (r), entonces, fuera de este volumen:
V ~ \sqrt{r} ».
((17) pág. 629).
Es evidente que, si la (G) del protio y del antiprotio es dos veces menor que el valor experimental más preciso obtenido con balanzas de torsión (54), entonces la masa virial del Universo es el doble de la calculada “…a partir de la luminosidad de las galaxias individuales y de la relación masa-luminosidad para las galaxias” ((17) pág. 623), (…y de la constante gravitacional obtenida con balanzas de torsión para metales, y no para el protio (Aut. N. N. Rozánov).
En el artículo “El Universo en tonos oscuros”, del doctor en ciencias físico-matemáticas y especialista en cosmonáutica L.V. Ksanfomaliti, se dice:
«Hasta los años 70, los astrofísicos suponían ingenuamente la existencia de la materia oscura solo en los cúmulos de galaxias. Luego se “admitió” también en nuestra galaxia, donde representa aproximadamente tanta masa como la materia ordinaria» [nota 1]. «…En este sentido, alrededor y dentro de nuestro sistema estelar se encuentra otra galaxia. La materia oscura no interactúa con ningún tipo de radiación, no emite luz y no absorbe nada. Pero está sujeta a la ley de gravitación universal [nota 2] y se manifiesta concentrándose alrededor de galaxias y otros objetos masivos. Sin embargo, sería más correcto decir que son las galaxias y otros objetos masivos los que se concentran alrededor de los cúmulos de la misteriosa materia oscura». (Revista “Universo, espacio, tiempo” Nº10, 2005, pág. 7).
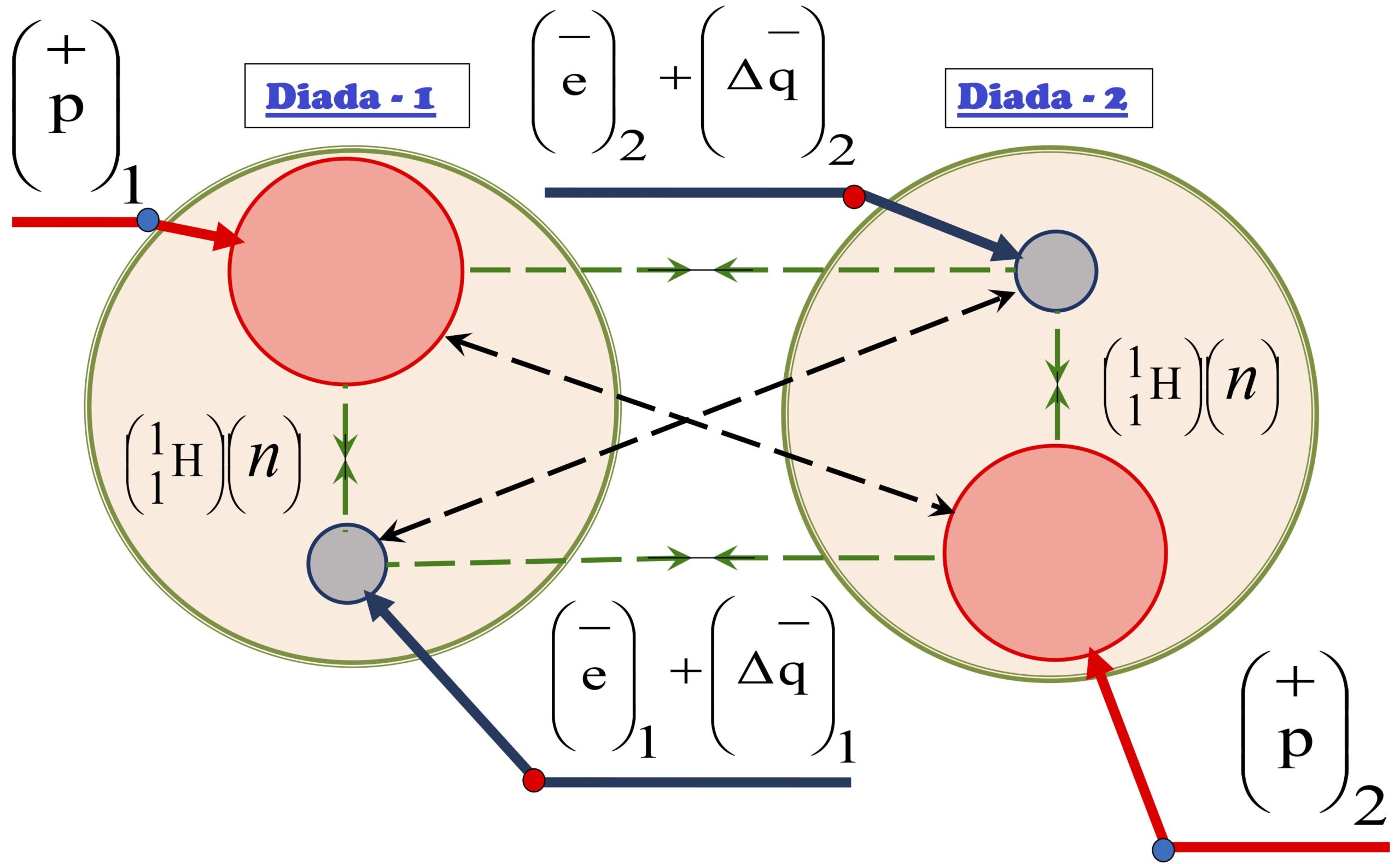
nota 1 Debe precisarse que no toda la materia “gravita”, sino solo aquella parte que se denomina “sustancia” (20). La “sustancia” posee una masa virial en reposo y una carga electrodinámica (magnética) excedente, es decir, está compuesta por diadas ligadas:
\left(\overset{\mp}{p}\right) + \left(\overset{\pm}{e}\right),
cuyas partículas, de acuerdo con el teorema del virial, giran alrededor de un centro de gravedad común con velocidades inversamente proporcionales a sus masas en reposo. Como resultado, surge una carga excedente con el signo del leptón de la diada, de magnitud:
\left(\Delta\overset{\pm}{q}\right) ≈ 1÷ 2 × 10-37(c).
nota 2 La “Ley de la gravitación universal” debería denominarse más bien “Ley de la interacción universal”, ya que la sustancia y la antisustancia se antigravitan entre sí (13), (43).
A partir del valor calculado del coeficiente gravitacional para el protio, la masa virial del Sol debe ser:
M(Sol)= 1,99 × 1030(kg) + 1,99 × 1030× 70% = 1,99 × 1030 + 1,3930 × 1030 ≌ 3,383 × 1030(kg)
((17) página 37).
El coeficiente gravitacional del helio es:
G = 6,213116227171935 × 10-11(N × m2 × kg-2)
(Véase Ejemplo 6 + Apéndice 6).
Por consiguiente, el helio-4 influye en menor medida en el valor de la masa virial del Sol, pero, en caso necesario, puede calcularse fácilmente (~+7% respecto al valor obtenido con la G estándar).
- Estimados visitantes, para dejar su comentario, no se requiere registro.
- La edición de fórmulas matemáticas en los comentarios se realiza en el sistema «LaTeX». Una fórmula se abre con la palabra katex [entre corchetes] y se cierra con /katex [entre corchetes].
- Si su comentario contiene un enlace, se enviará automáticamente a la carpeta de spam para su revisión. Sin enlaces, todos los comentarios se publican sin demora.